Prioritized Training with Reducible Holdout Loss
This post explores prioritized training, a curriculum learning technique that selects which training examples to focus on each epoch. By training on only the most “learnable, worth learning, and not yet learnt” datapoints, models can achieve similar performance while seeing ~90% fewer examples per epoch - essentially a speedrunning technique for neural network training.
Introduction
We will look at the paper titled “Prioritized Training on Points that are Learnable, Worth Learning, and Not Yet Learnt”
Core Question: Is it possible to train a classification network on a subset of the training data each epoch?
Simple Answer: Yes! In some cases, we can ignore ~90% of the datapoints in each batch and still get similar results.
Overview
The core of this paper is about how to select which datapoints to train on, and which datapoints to ignore. If the datapoints are chosen correctly, then the resulting network will be more accurate despite seeing a fewer total number of samples than the naively trained network, which sees every datapoint once per epoch1.
When is RHO loss most useful?
-
When you have plenty of data, but not enough compute. Selecting a smaller subset of points that are more likely to improve the model can help speed up training if compute is the bottleneck.
-
When the data is noisy or has a lot of outliers, the rho loss can help filter out those points. By ignoring these, we have a better chance at a healthier leaning dynamic.
-
Towards the beginning of training but not immediately after. When the weights are random, the target loss is more about noise in the network’s intialization more than the difficulty/usefulness of a given training point. However, the holdout loss part of the equation is still informative, and so the rho loss is still useful right off the bat.
When is RHO Loss not useful?
For this to work, we are basically using the rho loss as a proxy, and as such we should think about cases where the proxy is no longer useful.
-
The tradeoff with this style of curriculum learning is that the holdout model is static, and RHO loss loses a degree of freedom in that regard. Ideally the holdout model would always be just slightly more developed than the target model. In this case, even as our target model gets more advanced, the holdout model doesn’t change. Depending on where yoou want your speedrun to land, I’d say you want a model that is tastefully underfit.
-
At the limit, when you have a very good model and are trying to squeeze out the last few percentage points of accuracy, this method does not work very well. In fact, as soon as the model starts to get as good as the holdout model tne usefulness drops off.
-
When there is not enough data to have a separate holdout dataset, or when you are training on a small dataset in general.
The Ideal Datapoint
Assuming we are able to discard a great number of datapoints in any given batch, how do we determine which datapoints are ideal to train on at any given time? First, let’s consider what an ideal datapoint to train on would look like.
The ideal datapoint to train on has several properties - it is learnable, worth learning, and has not been learned.

Training Loss
To measure how much a datapoint has been learned during training, we can evaluate the target model on the point and use the loss. If a network has high loss on a datapoint, the datapoint has not been learned yet. Naively, we might just try training on datapoints that have high losses, but this introduces some issues.
There might be good reason why the training loss is high on a given datapoint. That datapoint could be mislabeled, an outlier, or just have a really bad signal to noise ratio. While these datapoints are have not been learned yet, they also are not worth learning. Since want to avoid training on these datapoints, we will need to find a way to filter them out, which is where the holdout model comes into play.
Irreducible Holdout Loss
The holdout model has the same or a similar architecture to the target model, and is trained on holdout data from the same distribution as the target model. Critically, the holdout model is not trained on any of the training data, and the target model is not trained on any of the holdout data.
We can evaluate the holdout model on a given datapoint in the training set, calling it the irreducible loss. This gives a measure of how well a fully trained network was able to learn the point - a measure of how learnable the datapoint is!
RHO-LOSS
Given these two measures - training and irreducible loss from evaluating the target and holdout models on a set of given training datapoint candidate - how should we combine the values to select for the most appropriate datapoints?
Introducing the reducible holdout loss, aka rho-loss.
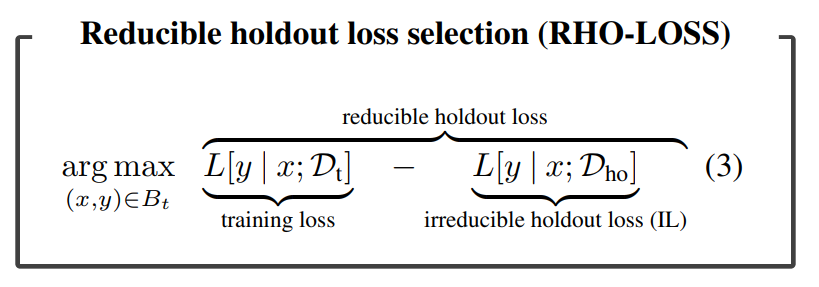
Looking at this equation, we see datapoints that are selected for will have high training loss and low irreducible loss. These points are desirable to train on because 1) the target model has not learned them yet, and 2) a similar network was able to learn them.
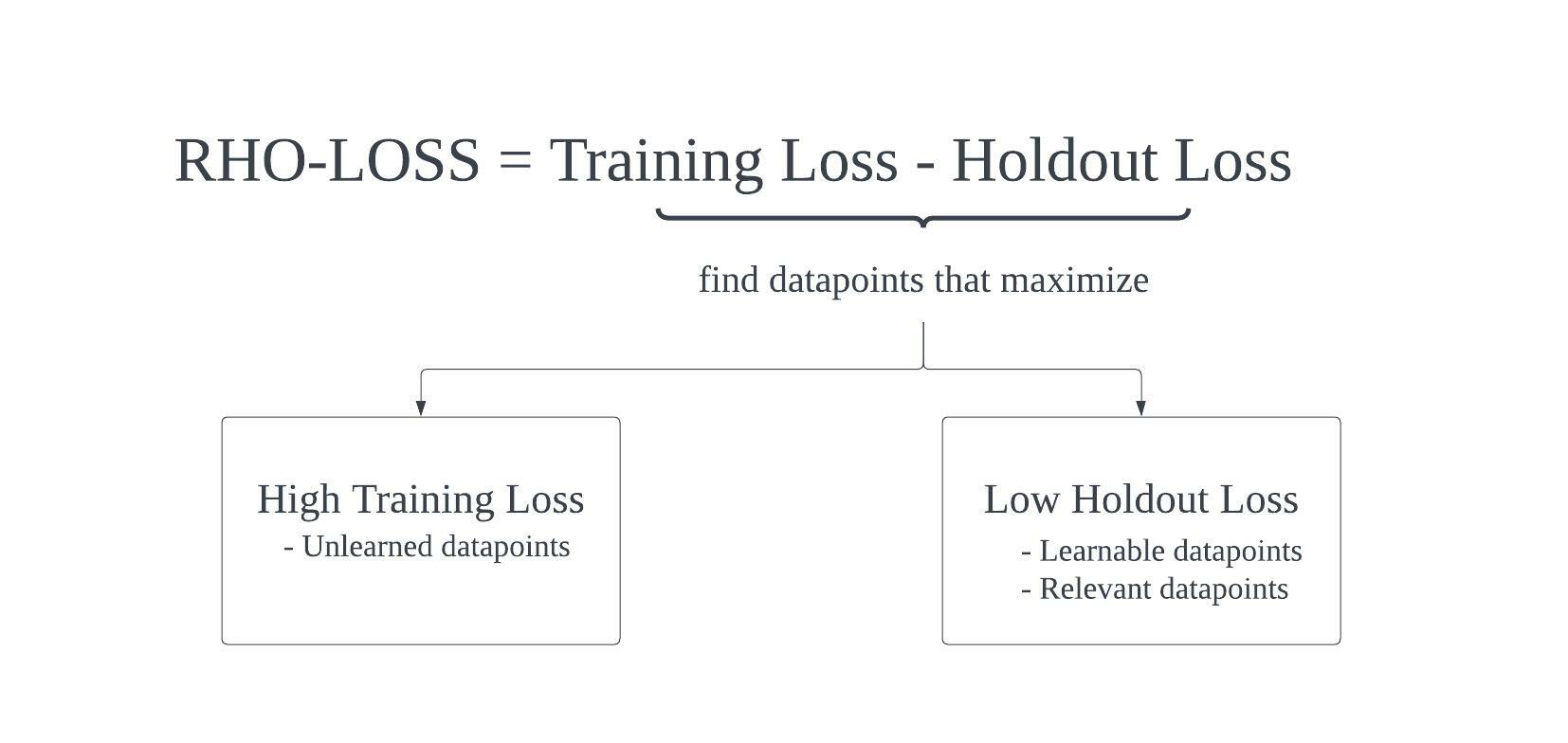
Datapoint Selection
Now, let’s consider how this equation filters out less desirable points (unlearnable, not worth learning, or already learnt).
Datapoints that are not selected for:
- Training loss is low. Since these datapoints have already been learned, the gradients will not update the weights very much, meaning the network is not learning anything new.
-
Training loss is high, but the irreducible loss is also high. If a datapoint has a high training loss and a high irreducible loss, this indicates that the datapoint wasn’t learned by the holdout model or the target model. When does this occur? It can occur if the datapoint is noisy, mislabeled, or an outlier. The datapoint is not learnable.
- Training loss is low and the irreducible loss is high. This case is unusual but can occur more frequently towards the end of training. A rarer case that indicates your model already fit a datapoint better than the holdout model. This datapoint is not worth learning.
Algorithm
Now that we have the intuition behind what makes a data point desirable and a way to measure it, let’s look at how this works
Step 1: Train the holdout model on the holdout data. Keep this network in memory for the time being.
Step 2: We then evaluate the holdout model over all the available training points, creating the irreducible losses, which the paper calls the irreducible loss. Critically, this happens just once before training the target model.
Step 3: With the irreducible losses in memory, shuffle/prepare the data to train the target model.
Step 4: Load a batch of candidate datapoints, which will be N times bigger than the actual training batch, depending on your desired subsampling rate2. Then, evaluate the current model against each candidate point to find the training losses3.
Since we precomputed the irreducible loss (holdout model against the training data), we can now use the training losses and irreducible losses to calculate the rho-loss for each point in the candidate batch.
Step 5: Select the points from the candidate batch that have the highest rho loss to form the training batch.
Step 6: Train the target model on the training batch, do the weight updates, and go back to step 4 until training is finished.

Notes
While it might seem inefficient to train a whole other network just to train our target faster, we only need to train the holdout model once and can reuse it for many target networks.
Intuition
Different datapoints have different levels of usefulness depending on where we are in training. In the early epochs of training, easier datapoints will be more useful, and later on in training, harder datapoints will be more useful 4.
Training on datapoints that are perfectly in the center of the manifold the network has already learned will produce very small losses, small gradients, and thus negligible changes to the weights, wasting an update. Conversely, training on datapoints that are too far out of the manifold will result in large, noisy gradients that may be counterproductive. The rho-loss function balances these two opposing forces to get a higher signal gradient update.
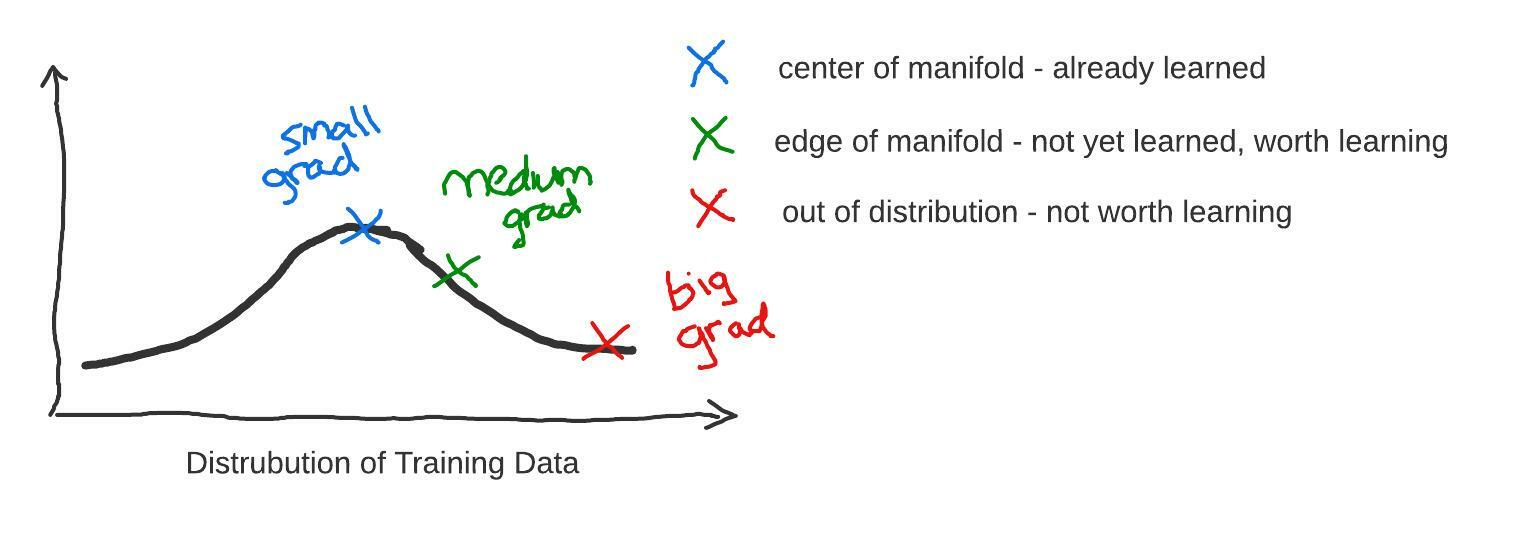
Ideally the holdout model is getting data from the same distribution as the target model, but not the same data points. When calculating the RHO loss, we evaluate the holdout model on the training set, data it has not seen.
This helps us know whether that datapoint is in the distribution of an underfit model rather than being memorized by the holdout model. If the datapoint is perfectly in distribution, then it will be similar to datapoints the holdout model has seen, and the irreducible loss will be low. Conversely, if the datapoint is mislabeled, an outlier, or otherwise having a bad signal to noise ratio, the irreducible loss will be high.
Summary
Instead of having the model focus on learning datapoints of all difficulties all at once, prioritized training focuses the model on learning a smaller subset of carefully selected datapoints.
We should mentally classify prioritized training as a speedrunning technique more than something that will always improve performance. It’s fair to say this is true in people too; learning a subject the fastest is not the same as learning it the most deeply.

Footnotes
Keywords: active learning, curiculum learning, dataset distillation, prototype learning
-
Over the course of training, the points that are the most useful to train on will change. As a result, the model will most likely see every datapoint over the course of training, it just will not see every datapoint every epoch. Note that in this context, an epoch is an iteration over the whole dataset where each datapoint is part of a candidate batch, rather than each datapoint being part of a training batch. For example, if our training batch is 10% of the size of the candidate batch, then then we only end up training on 10% of the datapoints in an epoch, even though 100% of points were considered. ↩
-
If you want a training batch size of 64 composed of the top 10% of the datapoints in each training batch, there would be 640 datapoints in the candidate batch. ↩
-
Most of engineering implementation complexity comes from doing this in a way that doesn’t severely slow down the data loading process, since it requires using an up to date copy of the target model ↩
-
I support this claim by noting that using an underfit holdout model seems to give better performance in the earlier epochs of training compared to using a well fit holdout model ↩